Page 2.  Refractive Index, Angular Aperture and N.A.

1. Diffraction, Resolution. 2. R.I. and N.A. 3. Magnification.

Although microscopists had known for most of the 19th. century that the resolving power of a microscope objective was dependent upon its angular aperture, this could not be used as a measure of resolution since it varied greatly depending on the refractive index of the medium through which the image-forming rays passed.
It was equally clear that the information contained in the cone of image-forming rays did not change, even though the angle of the cone did.

It was Ernst Abbe (1840 - 1905) who first described the relationship between image resolution, angular aperture and refractive index of medium. He called the new measure of objective performance "Numerical Aperture" or N.A., and defined it thus:


where Ø is the angle the ray makes with the optical axis (half the value of the angle of the image-forming cone), and R.I. is the refractive index of the medium through which the rays pass.
It is clear that Ø can never be larger than 90°, and since sine of 90° is 1, no objective can have an N.A. numerically larger than the R.I. of the medium in which it is working.
This implies an acceptance angle for the frontlens of the objective of 180°. In practice, the largest angle of acceptance of glass lenses in any medium is around 140°, so the N.A. of an objective is always less than the theoretical maximum.

Consider the diagram below which represents a dry objective of N.A. = 0.95 examining a specimen in water under a coverglass. The acceptance angle of this objective is 144° in air, which becomes 77° in the coverglass, and 91° in the water containing the specimen. Even though the specimen may have detail producing first order maxima at a greater angle than shown, these rays (in blue) cannot escape the glass-air surface of the coverglass. They strike this interface at too oblique an angle for refraction, and are totally internally reflected back into the glass.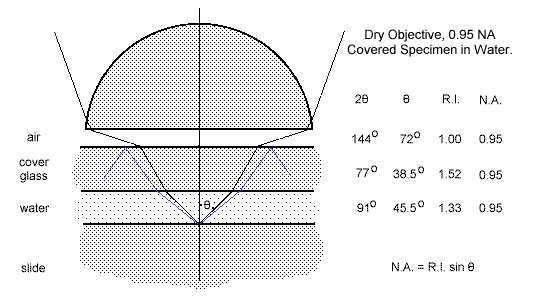




If the dry objective of 0.95 NA were replaced with a water immersion objective of 1.25 NA, and the space between the coverglass and the frontlens filled with water, the acceptance angle of this objective in the immersion water is 143°, which, after refraction through the coverglass, is also 143° in the specimen water. This results in the gathering of a far larger solid cone of diffracted light than was possible with the dry objective, and hence an image with finer detail. The increase in detail revealed is directly reflected in the difference between the two N.A.s.
In the diagram below, the thickness of the water film, the thickness of the coverglass and the working distance of the objective have been left unchanged in order to show the increase in diameter required to produce a frontlens capable of collecting the wider aperture cone. In the real world, the dry objective would have a magnification of about x40, a longer working distance on the scale of the diagram, and hence larger diameter than shown. The water immersion objective of NA 1.25 would have a magnification of about x70, and therefore a shorter working distance.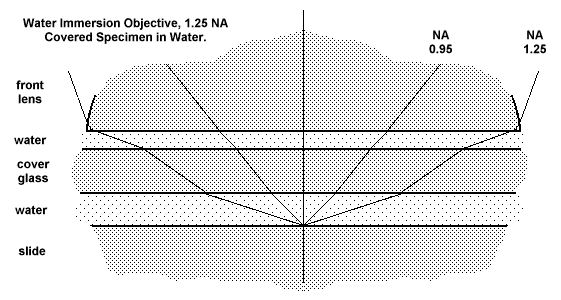




Abbe extended this thinking to a situation in which the entire space between the specimen and the objective frontlens was filled with a medium having the same refractive and dispersive qualities as the glass of the frontlens. He found a medium of the required properties in cedarwood oil, and the oil-immersion objective began its career. For certain specimens, such as stained bacterial smears and blood films, the coverglass could be dispensed with, and it exerted no refractive effect upon the image-forming rays from a specimen mounted in balsam. Because of this continuity of optical properties in the object space, the system was also called "homogeneous immersion".
It enabled the highest resolution possible for an objective having a glass frontlens. The diffracted rays from the specimen passed undeviated into the glass of the frontlens, undergoing their first refraction at the strongly curved upper surface. An advanced tutorial deals with the way Abbe made use of this situation to solve the otherwise difficult problem of spherical aberration in such a powerful frontlens.

For the present business of image formation, it remains only to deal with the not-so-obvious relationship between magnification and image sharpness.